執筆:天野由貴 監修:奥村晴彦

はじめに
この連載では,世の中に出回っている変なグラフを例に,どこが悪いかを解き明かしていきます。みなさんも変なグラフにだまされないよう,イトウさんとにゃんこさんと一緒に学びましょう。
人物紹介

奥村先生
言わずとしれた,すんごい先生。統計学,物理学,情報学に精通しており,LaTeXやRの本も執筆されている。にゃんこさんとイトウさんをやさしく指導してくれます。

にゃんこさん
わかりにくさを嫌う猫。グラフはわかりやすくしてほしいと常日頃思っている。3Dグラフは撲滅!撲滅!!

イトウさん
本連載では生徒役。すべてのことをわりとあっさり受け止めるタイプ。
前回までのあらすじ
前回は棒グラフでした!
イトウさんが成長してきましたね!
折れ線グラフ
今回は折れ線グラフです
折れ線グラフでありがちなのはこんなやつです
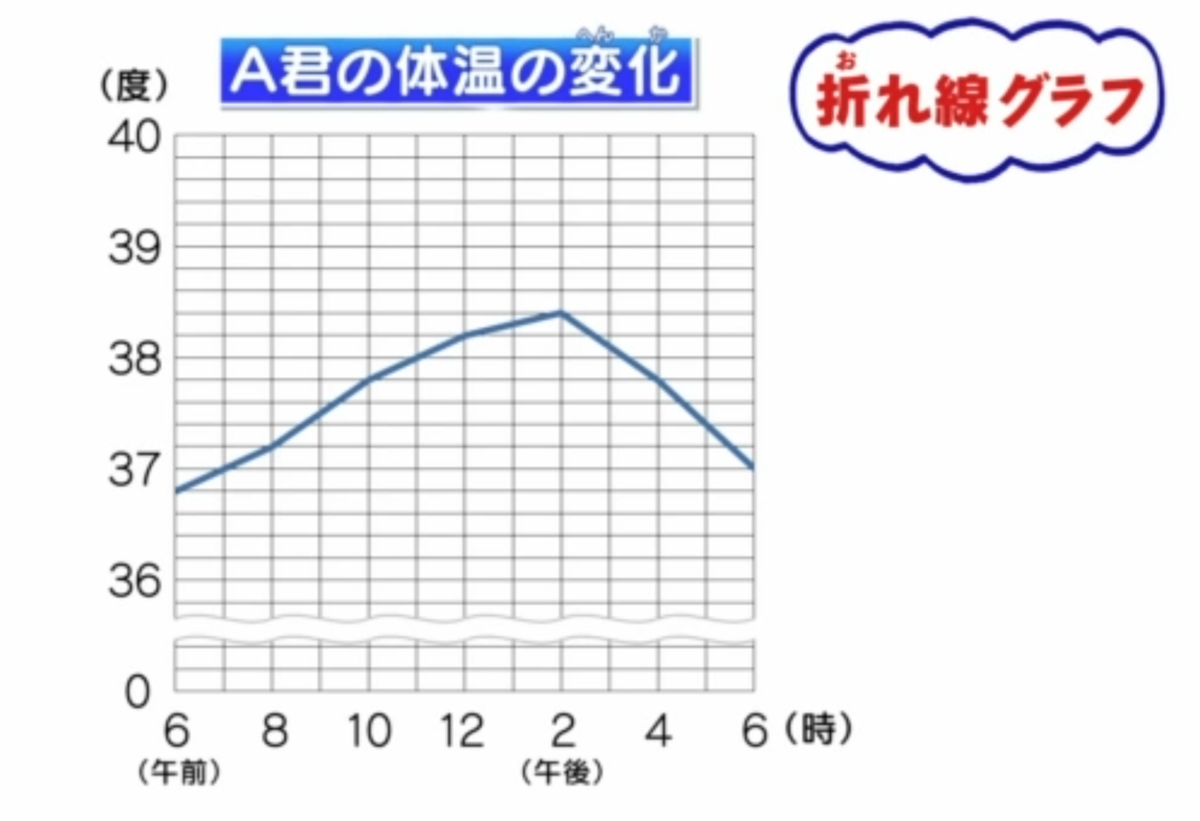
出典:NHK for School
http://www2.nhk.or.jp/school/movie/clip.cgi?das_id=D0005320371_00000
わかった!この省略線がまずいんですね?0からちゃんと省略せずに書かないといけないですよね!
イトウさん,実は・・・折れ線グラフは0始まりじゃなくてもいいんです!
な,な,なんと~!
棒グラフは,棒の面積で量を比べるので,省略すると誤解をまねくんですよね。でも,折れ線グラフは,点の位置で量を示すので0始まりでなくてもいいんです
じゃ,この省略線は意味ないってことに・・・
そのとおり!
そんなわけで,省略線なしで描いてみました
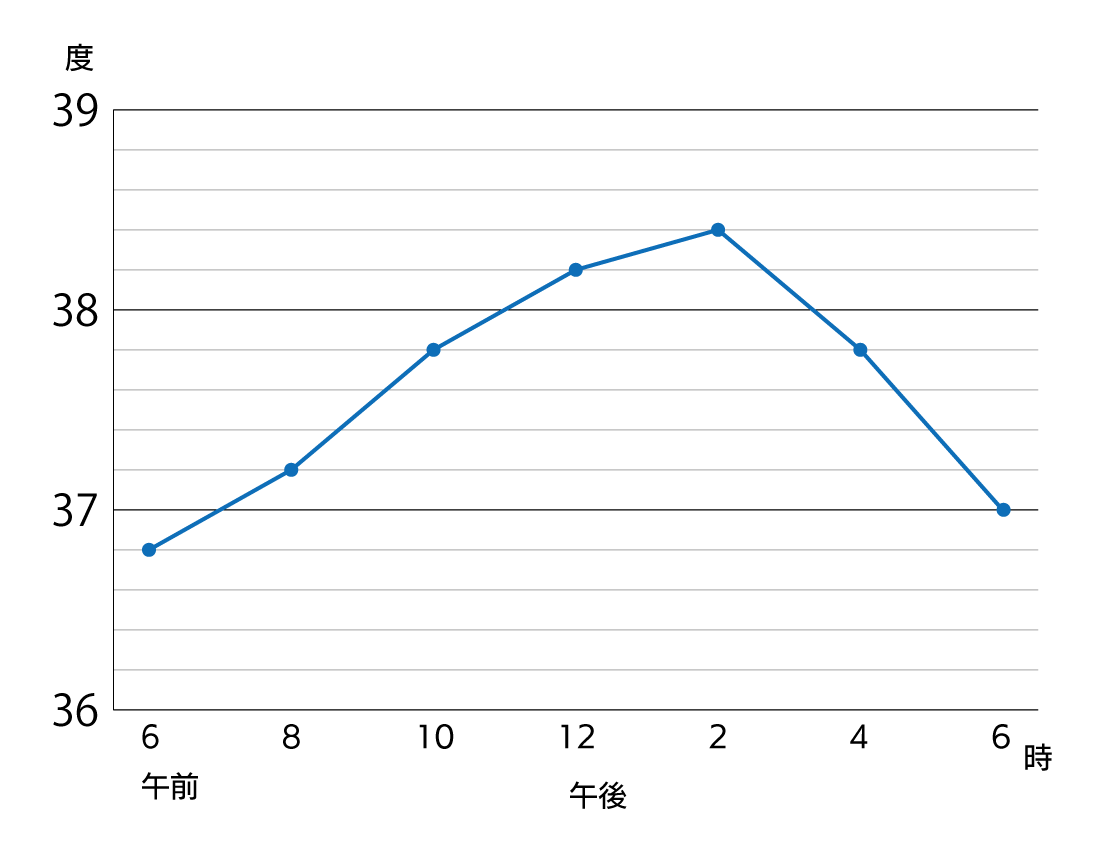
にょろにょろ無しで美しい!
折れ線グラフにはにょろにょろ省略線はいらないですね
(実は前回の防衛関係費のグラフも0はじまりじゃなかったけど・・・)
(あっ・・・)
尺度とグラフの関係性
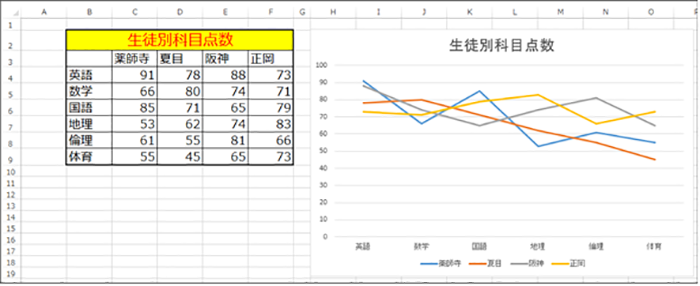
出典:@IT
https://www.atmarkit.co.jp/ait/articles/1410/09/news033.html
これは,なんで折れ線グラフにしちゃったんだろう,てやつですね
横軸のデータが名義尺度なので,折れ線グラフには向かないですね
名義尺度?ってなんですか?
この連載をもう6回分も読んでくださってる読者のみなさんは,かなり成長されてると思いますので,ここでグラフの基になるデータの尺度(尺度水準)について学びましょう!
奥村先生 特別コラム「尺度とは?」
データの性質には4通りの「尺度」というものがある,ということを※スティーブンズという人が唱えています。
※Stanley Smith Stevens(スタンリー・スミス・スティーブンス 1906年11月4日 - 1973年1月18日)は,ハーバード大学の音響心理学研究所を設立し、音響心理学を研究したアメリカの心理学者。
順序関係のない単なる名前や番号
例:生徒名や出席番号,科目名など
順序に意味があるが,間隔に意味がないもの
例:順位,好き/ふつう/嫌いなど
数値の差に意味があるが,比に意味がないもの
例:セ氏温度(°C),西暦年など
数値の差だけでなく比にも意味があるもの
例:重さ,長さ,降水量など
この分類にしたがえば,上で出てきた「A君の体温」は間隔尺度のデータです。間隔尺度のデータには「0」に特別な意味がありません。つまり,「0°C」の「0」に意味がないのです。
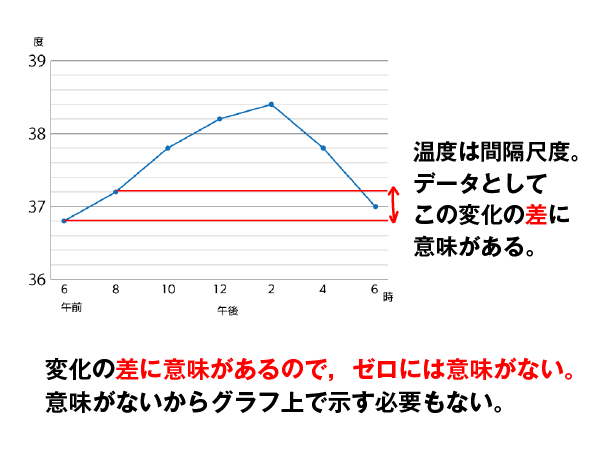
英語圏の国でよく使われている※カ氏温度(°F)の0度は,セ氏温度(°C)の0度とまったく違う温度であることからも,温度の「0」に意味がないことがわかると思います。40°Cの水は20°Cの水の2倍熱いわけではありません。
※日本で主に使われるセ氏温度(°C)の0度は,カ氏温度(°F)に変換すると32°Fとなります。そして0°Fは-17.778°Cです。基準が全く異なっていますが,どちらも温度の表現です。
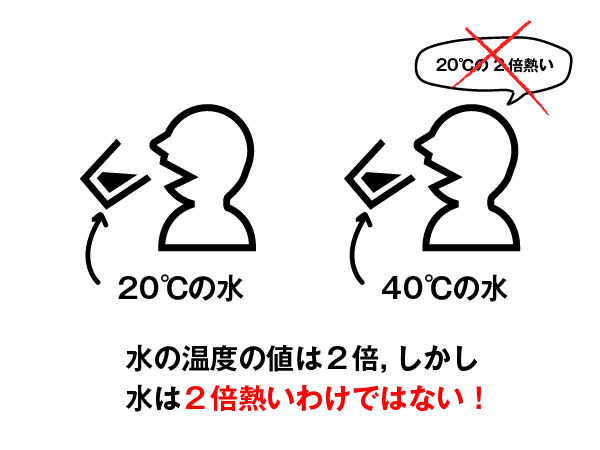
棒グラフは0から始めると言いましたが,0に意味があるのは比例尺度だけなので,棒グラフは比例尺度の量を描くときだけ使います。温度のような間隔尺度の量は棒グラフで表さないのです。
折れ線グラフは0から始める必要がないので,間隔尺度の量を表すのに適しています。地理で気温と降水量のグラフを描くときも,気温は折れ線グラフ,降水量は棒グラフをよく使いますね。
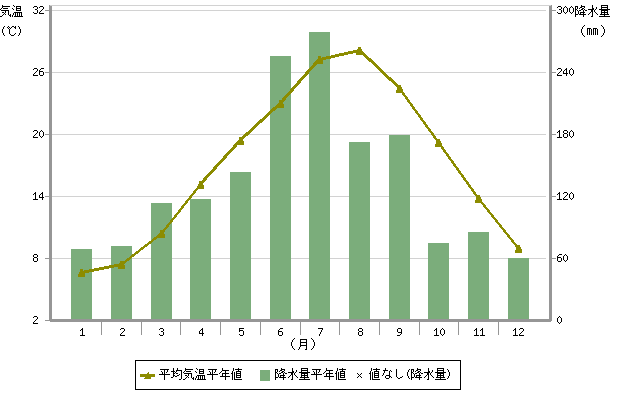
参考出典:気象庁 『地点別平年値データ・グラフ』より
・ ・ ・。

イトウさんがフリーズしている・・・。
さっきの成績のグラフは,なにかの変化を表しているわけではないですよね。もう一度見てみましょうか。

イトウさんが前回言ってたように,折れ線グラフは変化を見るのに向いているので・・・
そうか!英語、数学・・・は名義尺度で,変化をしていない。だから変化をあらわす折れ線グラフは向かないんだ~なるほど~
でも、これはどういう風に描きなおしたらいいんですか?
そこが難しい問題です
そもそも4人の成績をこんな風に比べたいニーズがあまり無いように思います
ひとりひとりの傾向を見たいんだったら,レーダーチャートが向いてますけど・・・
教科間でテストの難易度が違う可能性があるので,素点で比べるのはレーダーチャートに向いていないですね。
・・・もうちょっと詳しくお願いします!
つまり,同じ60点でも,平均40点なのか平均80点なのかで,テストの難易度が変わります。順位か偏差値のように比べられる量のほうが,それぞれを正しく比較できますね
えーっと・・・つまり点数を比較するテストの場合は,難しさはそれぞれ異なっているから,相対的に比較できるように偏差値や順位を用いる・・・ということですか?
いいですね,イトウさん!そのとおりです!!
でも,4人分の偏差値とか出してもあまり意味なさそう
50人くらいの成績だったら,2科目で点数を散布図にするとかもありますが,4人だし・・・
今回は描き直しグラフなしで!!
そ,そんなパターンもあるんですね!?
まとめ
今回は,折れ線グラフは0はじまりでなくてもいい,が衝撃でした。
あと尺度を理解するのに苦労しました・・・。
そして完全に理解できたという自信はありません・・・。
A君の体温のグラフでは,折れ線グラフは0から始めなくていいということと,0に特別な意味がない量だからこそ折れ線グラフを使うということを,両方学べます。尺度の理解はとても重要なので,引き続き頑張りましょう。
なんでそのグラフを使うか,ということを尺度を意識しながら考えられるようになりたいですね
うっ,がんばります・・・
次回も折れ線グラフについてやります!
著者プロフィール
天野 由貴(アマノ ユキ)
大学職員。インストラクショナル・デザインの研究者。「情報デザインを意識したスライド作成入門」等の教材を作成・公開。ねこが大好き。 https://home.riise.hiroshima-u.ac.jp/~ten/
奥村 晴彦(オクムラ ハルヒコ)
三重大学特任教授。統計学,情報科学,情報教育の研究者。 第一学習社の「情報」教科書の著者の一人。 https://oku.edu.mie-u.ac.jp/~okumura/